|
GR0177 #39
|
|
|
Problem
|
|
|
This problem is still being typed. |
Electromagnetism }Filters }Filters
High-pass filters have, for high-frequencies (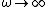 ), ),  . .
The net impedance is given by 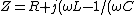)) . . 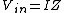 , and thus , and thus 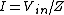 . .
For cases I and II, 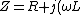) . .
For case I: 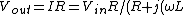)) Thus, in the regime of high, frequency, one gets Thus, in the regime of high, frequency, one gets 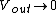 (This is a low-pass filter.) (This is a low-pass filter.)
For case II: 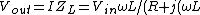)) , one gets , one gets  (To wit: L'Hopital's Rule can be used or this limit.) (To wit: L'Hopital's Rule can be used or this limit.)
For cases IV and III, )) . .
For Case III, ))) For high-frequency, For high-frequency,  \rightarrow 0) , and thus one has , and thus one has  . .
For Case IV, 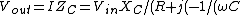))) . This quantity goes to 0 for high-frequency. (This is a low-pass filter.) . This quantity goes to 0 for high-frequency. (This is a low-pass filter.)
Hence, the only choices that work for high-freq filters are choices II and III. Choice (D).
|
|
|
Alternate Solutions |
secretempire1
2012-09-04 11:09:51 | The main answer for this question comes off as more mathematical than it needs, in my opinion (Ironically, my explanation is longer, but more qualitative). Just for those who don't know a great deal about voltage and circuits, across those two circuit elements in each picture, there must be a drop in voltage equal to the source voltage. For example, if I put a 10 Volt AC (RMS) source into the circuit, there will be a 10 volt drop across the two elements.
In these 4 scenarios, you are measuring the voltage drop across only one of the elements (labeled 'OUT'). The goal of a high pass filter is to, at high frequencies, measure a greater voltage drop across the measured element, compared to the other one. What causes a higher voltage drop is a higher impedance of the circuit element. Therefore, you want the element being measured to have a higher impedance than the other one.
The impedance of a resistor (zig zag) is just equal to its constant resistance R. It has no dependency on frequency.
The impedance of a capacitor (two parallel lines) is proportional to 1/f.
The impedance of an inductor (spirals) is proportional to f.
So take a look at circuit number I:
Since the impedance of the inductor rises with frequency, there is going to be a relatively higher drop across the inductor than the resistor. This means that you will measure a SMALLER drop across the resistor. Therefore, this IS NOT a high pass filter.
II:
As f increases, the inductor will have a higher impedance than the resistor, meaning a greater voltage drop across the inductor. You are measuring the drop across the inductor, so higher frequencies will result in higher measurements. This IS a high pass filter.
III:
As f increases, the impedance of the capacitor decreases, meaning a larger drop is measured across the resistor. This IS a high pass filter.
IV:
As f increases, the impedance of the capacitor decreases, meaning a larger drop is measured across the resistor. But you are measuring the capacitor in this case, meaning you will measure a smaller drop. This IS NOT a high pass filter.
|  |
|
|
Comments |
dberger8
2016-07-06 22:20:19 | My answer is a bit more clear, and less algebra.\r\n\r\nFrom Ohm\'s law, we have that\r\n\r\n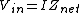 and and  , where complex notation is being used. Dividing the two equations we get that \r\n\r\n , where complex notation is being used. Dividing the two equations we get that \r\n\r\n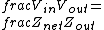 \r\n\r\nIn the limit, we desire that this ratio be unity. Hence, high pass filters require that in the limit as \r\n\r\nIn the limit, we desire that this ratio be unity. Hence, high pass filters require that in the limit as  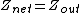 . Clearly, this is only true of answer (D). . Clearly, this is only true of answer (D). |  | calcuttj
2014-09-26 07:31:40 | A High pass filter has Vout -> Vin at high freq and Vout -> 0 at low freq. So look at impedances.
Resistors don't change impedance with frequency change.
For a Capacitor: Z = -i/ C, so at high frequencies the impedance is low (essentially zero in limiting cases) and the potential drop (via generalized ohm's law V = IZ) is then 0. Thus, a capacitor can't be the element for Vout in a high-pass filter -> eliminate IV choose III C, so at high frequencies the impedance is low (essentially zero in limiting cases) and the potential drop (via generalized ohm's law V = IZ) is then 0. Thus, a capacitor can't be the element for Vout in a high-pass filter -> eliminate IV choose III
Inductor: Z = i L: high frequency -> high impedance -> high potential drop -> this can be the element for Vout ->II is good, eliminate I L: high frequency -> high impedance -> high potential drop -> this can be the element for Vout ->II is good, eliminate I
|  | secretempire1
2012-09-04 11:09:51 | The main answer for this question comes off as more mathematical than it needs, in my opinion (Ironically, my explanation is longer, but more qualitative). Just for those who don't know a great deal about voltage and circuits, across those two circuit elements in each picture, there must be a drop in voltage equal to the source voltage. For example, if I put a 10 Volt AC (RMS) source into the circuit, there will be a 10 volt drop across the two elements.
In these 4 scenarios, you are measuring the voltage drop across only one of the elements (labeled 'OUT'). The goal of a high pass filter is to, at high frequencies, measure a greater voltage drop across the measured element, compared to the other one. What causes a higher voltage drop is a higher impedance of the circuit element. Therefore, you want the element being measured to have a higher impedance than the other one.
The impedance of a resistor (zig zag) is just equal to its constant resistance R. It has no dependency on frequency.
The impedance of a capacitor (two parallel lines) is proportional to 1/f.
The impedance of an inductor (spirals) is proportional to f.
So take a look at circuit number I:
Since the impedance of the inductor rises with frequency, there is going to be a relatively higher drop across the inductor than the resistor. This means that you will measure a SMALLER drop across the resistor. Therefore, this IS NOT a high pass filter.
II:
As f increases, the inductor will have a higher impedance than the resistor, meaning a greater voltage drop across the inductor. You are measuring the drop across the inductor, so higher frequencies will result in higher measurements. This IS a high pass filter.
III:
As f increases, the impedance of the capacitor decreases, meaning a larger drop is measured across the resistor. This IS a high pass filter.
IV:
As f increases, the impedance of the capacitor decreases, meaning a larger drop is measured across the resistor. But you are measuring the capacitor in this case, meaning you will measure a smaller drop. This IS NOT a high pass filter.
griffitz
2012-11-05 19:41:10 |
This was incredibly helpful...thanks.
|
|  | J_21
2011-04-27 14:51:52 | Does anyone know of a textbook that covers this material? I haven't learnt these sorts of circuits in any of my classes and its not quite covered in my first year textbook, fundamentals of physics, either.
TylerClark
2011-06-24 15:21:40 |
Just read the first two chapters of Horowitz & Hill's "The Art of Electronics" you'll get everything you want to know about filters, and a little bit about complex impedances.
|
|  | istezamer
2009-10-12 23:38:09 | Actually I like how Yosun always reach for the mathematical approach to give you a profound solution that accepts no doubt!!... but at the same time I like the other approaches of the users... these are frequently time saving especially at the test when the average time you need to solve a problem is only 100 seconds!! |  | chrisfizzix
2008-09-23 08:25:58 | The easiest way to solve these kinds of questions is to remember the behavior of circuit elements in the high-frequency and low-frequency extremes.
At low frequency (aka DC), a capacitor just looks like an open circuit, while an inductor just looks like a wire.
At high frequency, a capacitor looks like a wire while an inductor looks like an open circuit.
Thus, we want the two circuits which have terminals that look like open circuits at high frequencies:
II has leads across the inductor, so that will pass HF.
III has a capacitor, which will look like a wire, and the resistor then sees all of the voltage drop.
Thus, answer D is correct.
In I, the inductor will appear open circuit ( ), so all the voltage drop will appear across the inductor and not the leads. ), so all the voltage drop will appear across the inductor and not the leads.
In IV, the capacitor will look like a wire, and no voltage drop appears across an ideal wire.
jmason86
2009-07-15 18:21:36 |
This is exactly how I did the problem. It's really quick and intuitive. Good explanation :)
|
wittensdog
2009-10-09 14:41:57 |
Very much agreed. When a problem doesn't specify any numbers, I think it's generally a hint that you shouldn't be thinking too much about math. The first time I went to do this I used roughly this method, not even really remembering anything about high and low pass filters, and managed to get it right.
|
walczyk
2011-04-07 07:58:38 |
this is an area that I am just very bad at. For case IV, how does this work as a low pass filter? You say it acts as a wire for high freq, so how does having a resistor across two wires work as a low pass filter? I don't even really understand the diagram too well, I wish I was taught this. I made a little mnemonic though; I only consider high pass filters cause H comes before L, and the L of an inductor is straight and vertical, and corresponds to the vertical section of wire in the diagram of the high pass filter.. it works for me albeit being very minimal
|
|  | blue_down_quark
2008-09-02 01:31:53 | A fast way to solve this problem is to note that for a high-pass filter the output will be zero if the input is DC . Only II and III fulfill this requirement. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
