|
GR0177 #37
|
|
|
|
|
Alternate Solutions |
wikiwert
2010-10-05 12:13:13 | Counterclockswise: negative work.
Area: the surface is an approximate triangle and V_B ~ 4.
Then W = Area ~ - (500 -200) * (4-2)/2 = -300 |  | scottopoly
2006-11-02 21:59:29 | To expand on herrphysik who has given a very good & quick solution:
We still do not know that the diagram is to scale, but: since we know P & V at C, and since we know P at B, and since  from C -> B, we can quickly get from C -> B, we can quickly get  . Then we can quickly calculate the area of the triangle, knowing the answer will be less than that. Luckily the area is . Then we can quickly calculate the area of the triangle, knowing the answer will be less than that. Luckily the area is 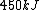 . . |  | herrphysik
2006-09-23 17:07:08 | I think the easiest way to do this problem is to just estimate the area within ABC. Looking at the graph, point B is at about 4.5. So if you take the box that AB and AC form, the area within ABC is a little less than 1/2 that...more like 1/2.5. Thus, 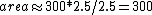 . And since there is work done on the gas here it is -300. . And since there is work done on the gas here it is -300. |  |
|
|
Comments |
cquinone
2018-10-04 19:26:08 | The area estimations I\'m seeing here and in other solutions are wrong, you can easily calculate the range of V to be 2-5, so area should be estimated as 1/2(b)*(h) = 1/2(5-2)(500-200)= 1/2(900) = 450. This is equidistant to 300 and 600, but you know that your estimate was slightly high as the isotherm BC dips down. So you pick -300. |  | omidkhakpour
2014-02-07 08:12:44 | by concept integral and work (p*v) you can eliminate a and b and c and e (total area cyclic is negative.b to c is negative. a to b is positive and more from a to b and less from twice a to b)
note: you need work done by the gas no by environment
you mus calculate just volume of b
|  | wikiwert
2010-10-05 12:13:13 | Counterclockswise: negative work.
Area: the surface is an approximate triangle and V_B ~ 4.
Then W = Area ~ - (500 -200) * (4-2)/2 = -300
wikiwert
2010-10-05 12:15:55 |
This is similar to what herrphysik said 4 years ago : P.
|
|  | physicsman
2010-01-27 22:23:17 | Q=W= (negative the area inside the loop)
Anyway you want to guess that area is the issue. Its kinda lame without the scale but -300 is the best guess just eyeballing it. |  | umichfan1
2006-11-26 17:23:02 | I came up with the exactly the same solution as the one given by this website, but isn't it a little weird that it wasn't one of the choices? Is it common for ETS to omit the true solution, give various other alternatives, and then ask us to select the one which is "most nearly" correct?
dillon
2008-09-05 10:40:31 |
I think in this particular case ETS didn't give the true answer because there is no reason to actually deal with logs. Since it is isothermal, it is easy to recognize that B must have a volume of 5. Since the work done from A to B is 300 kJ and the work from B to C has to be less than minus 300 kJ and more than -450, the best answer is clearly D. No real calculations at all.
|
realcomfy
2008-09-27 03:57:55 |
I'm sorry, but I don't understand where you came up with the work needs to be greater than -450kJ. I guess what I am still confused about is how are we supposed to estimate the value of the log function?
|
alemsalem
2010-10-04 12:04:16 |
it's just a little smaller than one, 5/2 or 2.5 is very close to e which is almost 2.7 so ln(2.5) is not far from 1
|
|  | scottopoly
2006-11-02 21:59:29 | To expand on herrphysik who has given a very good & quick solution:
We still do not know that the diagram is to scale, but: since we know P & V at C, and since we know P at B, and since  from C -> B, we can quickly get from C -> B, we can quickly get  . Then we can quickly calculate the area of the triangle, knowing the answer will be less than that. Luckily the area is . Then we can quickly calculate the area of the triangle, knowing the answer will be less than that. Luckily the area is 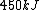 . .
realcomfy
2008-09-27 03:59:44 |
I like this solution, but I don't understand how we can, simply by estimating, know that the work is supposed to be negative. It is easy to find the area, but how do we know it is -300kJ and not positive?
|
mrmeep
2008-10-13 18:02:16 |
I have the same question as realcomfy; when we do the area method, how do we know the value should be negative and not positive?
|
wangjj0120
2008-10-27 01:19:55 |
It's easy, just rememer that if the diagram is clockwise, the work that the system does is positive, and it's negative otherwise.
|
sirius
2008-10-28 22:07:44 |
the gas does positive work in the expansion from A to B. It then does negative work from B to C. You can tell that the magnitude if the work from B to C is greater than the magnitude of the work from A to B by the fact that in addition to the compression work, there is also heat being added to the system, so more work must be done. This, then, is the reason why the work for the cyclic process is negative. This sort of thinking or careful thought of the area/integral approach can lead to the conclusion that CW cycles have positive work and CCW cycles have negative work.
|
anmuhich
2009-03-14 13:14:43 |
Yes, another easy way to see that it's negative is to notice that the pressure in the B -> C process is always higher than the pressure in the A -> B process. In general you can approximate work with a straight line with
W= P (deltaV) which means B -> C has the larger magnitude of the two. Since the gas is compressing in B -> C, it means that the gas is doing negative work because the convention is that when the gas expands it does positive work. So if you combine these ideas you get a net negative work.
|
nyuko
2009-11-04 23:25:25 |
Yeah, I did it this way too :D
|
|  | herrphysik
2006-09-23 17:07:08 | I think the easiest way to do this problem is to just estimate the area within ABC. Looking at the graph, point B is at about 4.5. So if you take the box that AB and AC form, the area within ABC is a little less than 1/2 that...more like 1/2.5. Thus, 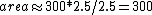 . And since there is work done on the gas here it is -300. . And since there is work done on the gas here it is -300.
grae313
2007-11-01 14:56:31 |
As scottopoly said,
You don't need to estimate V(B) for an ideal gas, just use 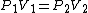 and solve for the unknown volume. and solve for the unknown volume.
|
|  | jax
2005-12-08 09:34:01 | How are we supposed to know that ln(2/5) ~ -1 without a calculator?
ymormy
2006-03-29 16:32:48 |
Maybe from this: we know =1) , and , and  . So . So <1) . So . So <1000) . So . So -600) cannot be 600. cannot be 600.
|
|  | ee7klt
2005-11-11 04:00:27 | Hi,
I think that there shouldn't be a minus sign in front of ) since since  < 0) ? ?
yosun
2005-11-11 14:24:40 |
ee7klt: thanks for the typo-alert; the typo has been corrected.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
