PHYSGOGO
2019-10-22 04:40:35 | oh sorry guys, I found another way: The energy to remove 2 electrons(79.0)= remove 1st+remove 2nd. Since remove 1st is under help of second electron\'s repel force. Removing second is 2^2*13.6=54.4 remove 1st=79-54.4=24.6 |  |
PHYSGOGO
2019-10-22 04:34:15 | since there are interaction between two electrons. we can solve in this way: STEP1: Remove two electrons(79eV) STEP2: pull one electron back(13.6*2^2=54.4eV) the result is also equals: ionize one electron. \\\\r\\\\nThe trick is, we can just calculate ionize energy of isolated electron, so we have to find a way isolate them. \\\\r\\\\nThe result is: 79-54.4=24.6 (we set remove is plus,pull back is minus) |  |
yummyhat
2017-10-25 21:06:50 | in case anyone is having trouble conceptually: the point is that helium is only hydrogen-like once it has already lost an electron. we are interested in the ionization energy of the first electron, but the approximation isn\'t valid there. hence we have to deduce its ionization energy from the information given in the problem. |  |
amirhse
2016-09-24 16:21:29 | For hydrogen-like ions: 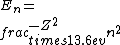 so we can calculate the energy for removing second electron by z=2 and n=1: so we can calculate the energy for removing second electron by z=2 and n=1:  , ionisation energy for removing inner (second) electron is , ionisation energy for removing inner (second) electron is 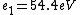 \r\nNow we have \r\nNow we have 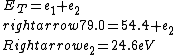 |  |
physgre
2015-10-15 02:40:59 | 两电子有排斥力,电离一个较容易。剩一个电子时,受核吸引,不易电离。
NervousWreck
2017-03-28 09:50:19 |
Yes very good man thanks.
|
EpicBradley129
2017-10-19 22:15:52 |
This answer is actually useful, except for the fact that it\'s in Chinese. So here\'s a translation (got this from a friend who studied Chinese in college):\r\n\r\n\"When two electrons repel each other, it\'s easy for one of them to ionize. When there\'s one electron left over, it is attracted by the nucleus, so it won\'t ionize so easily.\"
|
|  |
sina2
2013-08-26 02:33:59 | I solve this question in this way. First I compare a usual He with H atom. In H, it is 1 electron but in He there is 2 electron. So I spend x_1 energy to remove one electron to have just 1 electron for He to make it comparable with H. Now anything is same in two atoms, except the number of protons. I have Z=2 in helium. So by Bohr atomic model I calculate the energy should I spend to remove the remaining electron in helium.
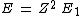 for ground state n=1 for ground state n=1
which
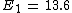
For Z=2 I find E=54.4. This is energy should I spend for removing the electron which is the same as Hydrogen's electron. Now I subtract the whole energy 79 to remove both electrons, from the energy I found to remove from ionized Helium.
79-54.4=24.6
x_1 = 24.6
The energy for removing the remaining electron in He is 54.4 which is more than the ground electron in H which is because of Z=2. |  |
EJtheDJ86
2011-07-28 07:33:53 | I thought of this problem in terms of an atom with a larger nucleus and many more electrons. Would it be easier or harder to remove the first electron or the very last one? Obviously the first will require less energy to remove and the very last will require the most. Thus for the current problem the first electron must be at least a little less than half of 79.0 or less than 39.5, leaving you with only A.
ali8
2013-10-04 07:19:22 |
Makes sense.
|
betagammalpha
2013-10-05 23:58:08 |
agreed
|
yummyhat
2017-10-25 20:50:04 |
good point
|
|  |
yaz
2010-10-05 21:31:50 | It takes 79.0eV to remove two electrons.
To remove the first electron, it takes less than 39.5eV (a half of 79.0eV) due to the effct of screening from the other electron. The only choise (A).
shak
2010-10-13 15:38:17 |
if u think that it is due to screening that energy will be less than half of total energy(79).
Can u show and prove it with screening?
|
Prufrock
2013-09-23 14:46:33 |
This seems like the best approach. Quantifying the screening effect is irrelevant (although the value is given by the other methods posted); you know that the electron "sees" less of the nucleus due to the other electron spending some of it's time between it and the nucleus, and thus it has a lower (less negative) binding energy and is easier to expel than the second.
|
|  |
star2009
2008-08-13 14:05:08 | E = -13.6 Z^2/n^2rnrn Energy to keep a first electron, Z=2 and n=1 for heliumrnrnSo rn E = -13.6 * 2^2 = - 54.4 e V.rnrnTotal energy to keep both electrons= total energy to remove both electrons = 79 eVrnrnEnergy to keep First electron = Energy to remove last electronrnrnSo that rn Energy to remove first electron = 79-54.4 = 24.6 eVrnrnrnAccording to "Nature", the least binding electron has to be removed first. The weaker the earlier...........rnrnNature is not fair. It is suck!!!!rn |  |
KarstenChu
2007-03-22 13:52:41 | I don't get this...in the second paragraph you state that E=Z^2E1 where Z=2 will be the ionization energy for Helium...so why do you have to subtract it from the energy require to remove both electrons to get the ionization energy for Helium? Don't you already have it? Respectfully, I do not believe this is the correct way to solve it and that carrie's rationale is closer to the mark.
kwooley
2007-09-27 20:47:44 |
KarstenChu - Though carrie's solution is a quick way to get the correct answer, I believe the original solution is correct. You are told how much energy is needed to remove both electrons. You can not apply the Bohr hydrogenic model to removing the first electron because He has two electrons. Thus you subtract the energy to remove the second atom from the total energy to get the energy it must have taken to remove the first electron.
|
|  |
carrie
2005-12-09 14:26:18 | It may also be useful to simply consider the fact that it will take more energy to remove the second electron than the first. Thus the energy to remove the first electron must be less than half the energy to remove both, and (A) is the only answer that it less than half of 79 eV.
Poop Loops
2008-10-31 22:18:24 |
Agreed. Calculating a number is the sucker's way of doing it.
|
walczyk
2011-02-25 21:01:24 |
I still think its easier on the brain to multiply 13.6 by 4 and take the difference from 79. You're going to need to know these equations for other questions on the test, so figure out the equations and the approximations (hc approx 1.98x10^-25 and R_infty is approx 1.097x10^7)
|
|  |
