|
GR9677 #31
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
Ryry013
2019-09-24 06:27:18 | For choosing between D and E, you can imagine dropping a feather vs a ball in air. A feather goes slowly, a ball goes quickly, so mass matters. Choose E. (See the other user answers for how to eliminate A-C). |  | Skribb
2009-09-26 04:57:38 | (A) Since the sphere starts at rest the kinetic energy must increase as the velocity increases to its terminal velocity.
(B) The sphere reaches a terminal velocity due to the retarding force but the retarding force doesn't completely stop the sphere, so the kinetic energy doesn't go to zero.
(C) It doesn't make physical sense for the sphere to exceed the terminal velocity and to then return back down to it, else it wouldn't be the terminal velocity.
(D) The description finally makes sense but we need to figure out what the velocity is dependent on. Set up your force diagram with the force of gravity pointing down and the retarding force pointing up, 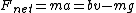 . Solve for v and you get . Solve for v and you get 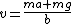 so v must be dependent on its mass, m, and the and the constant b. so v must be dependent on its mass, m, and the and the constant b.
(E) As per the explanation in D, v is dependent on b and m so this is the correct answer |  | jmason86
2009-09-21 20:19:44 | (A) (B) and (C) were all pretty easy to eliminate because they just don't make any physical sense.
The difference between (D) and (E), then, is just whether or not your speed will depend on your mass at all. Think limits: if you have 0 mass, then you have no surface area to drag with.. but I think this basically the buoyant force that the problem statement declares negligible. Hmpf. |  | dumbguy
2007-10-16 11:30:43 | Just think of it like a free falling object in which air is the vicous medium. What happens to a free falling object then will happen to this sphere, which leaves you at E. |  | keflavich
2005-11-11 11:15:19 | You can also recall terminal velocity happens when 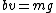 , i.e. when the acceleration is zero, which clearly shows that v depends on b and m. , i.e. when the acceleration is zero, which clearly shows that v depends on b and m.
u0455225
2008-06-22 14:32:03 |
This implies that equation given in part (D) has a sign error. mg-bv=0 when a=0, but the equation in part (D) contends (perhaps unintentionally) that mg+bv=0 when a=0.
|
physicsisgod
2008-10-28 15:53:26 |
u0455225, you are right. Which term is positive or negative depends on how you define the y-axis, but I would probably write 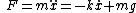 , where acceleration is positive in the negative-y direction. It doesn't really matter though, as long as they're opposite signs. , where acceleration is positive in the negative-y direction. It doesn't really matter though, as long as they're opposite signs.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
