|
GR9677 #100
|
|
|
|
|
Alternate Solutions |
dipanshugupta
2017-03-30 07:35:09 | If you have ever studied the Harmonic Oscillator, you\'ll know that  and and 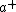 are Creation and Annihilation operators, i.e, they increase or decrease one quanta of Energy. \r\nI. The commutator gives one negative quanta of energy. \r\nII. Wrong if III is correct. \r\nIII. Definitely, as per above discussion. \r\n\r\nThus, answer is C. \r\n\r\n(I have taken a QFT class so it was easier for me but it\'s in QM too). are Creation and Annihilation operators, i.e, they increase or decrease one quanta of Energy. \r\nI. The commutator gives one negative quanta of energy. \r\nII. Wrong if III is correct. \r\nIII. Definitely, as per above discussion. \r\n\r\nThus, answer is C. \r\n\r\n(I have taken a QFT class so it was easier for me but it\'s in QM too). |  | oliTUTilo
2012-11-08 17:13:11 | For some constant k and integer m, 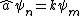 because because 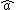 is said to return an energy eigenstate. is said to return an energy eigenstate. \psi_m) as well. as well.
So
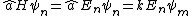
But
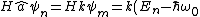 \psi_m)
So 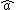 and and  don't commute. Since don't commute. Since 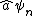 returns a different eigenstate of H, it returns a different state in general, so it can't be Hermitian. III is left, meaning we should answer (C), for Cake. returns a different eigenstate of H, it returns a different state in general, so it can't be Hermitian. III is left, meaning we should answer (C), for Cake.
|  |
|
|
Comments |
dipanshugupta
2017-03-30 07:35:09 | If you have ever studied the Harmonic Oscillator, you\'ll know that  and and 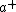 are Creation and Annihilation operators, i.e, they increase or decrease one quanta of Energy. \r\nI. The commutator gives one negative quanta of energy. \r\nII. Wrong if III is correct. \r\nIII. Definitely, as per above discussion. \r\n\r\nThus, answer is C. \r\n\r\n(I have taken a QFT class so it was easier for me but it\'s in QM too). are Creation and Annihilation operators, i.e, they increase or decrease one quanta of Energy. \r\nI. The commutator gives one negative quanta of energy. \r\nII. Wrong if III is correct. \r\nIII. Definitely, as per above discussion. \r\n\r\nThus, answer is C. \r\n\r\n(I have taken a QFT class so it was easier for me but it\'s in QM too). |  | hclmovie
2013-10-16 05:40:59 | extremely hard!!!!!!! |  | terry
2013-09-25 11:30:30 | There are actually lots of particulars like that to take into consideration. That could be a nice point to deliver up. I provide the ideas above as normal inspiration but clearly there are questions just like the one you convey up where a very powerful thing will probably be working in trustworthy good faith. I don?t know if finest practices have emerged around things like that, however I'm certain that your job is clearly identified as a fair game. Each girls and boys really feel the impact of only a momentâ?Ts pleasure, for the rest of their lives.
Terry http://www.qype.pl/people/artdri40
postal1248
2013-10-12 10:22:09 |
What are you talking about?
|
|  | oliTUTilo
2012-11-08 17:13:11 | For some constant k and integer m, 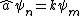 because because 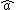 is said to return an energy eigenstate. is said to return an energy eigenstate. \psi_m) as well. as well.
So
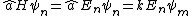
But
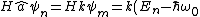 \psi_m)
So 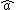 and and  don't commute. Since don't commute. Since 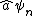 returns a different eigenstate of H, it returns a different state in general, so it can't be Hermitian. III is left, meaning we should answer (C), for Cake. returns a different eigenstate of H, it returns a different state in general, so it can't be Hermitian. III is left, meaning we should answer (C), for Cake.
|  | dstahlke
2009-10-09 12:02:42 | 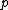 is observable and thus hermitian, so is observable and thus hermitian, so 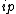 is anti-hermitian. A hermitian term plus a non-hermitian term is non-hermitian, in the same way that a real number plus a non-real is non-real. Remember, hermitian is like real, anti-hermitian is like imaginary and unitary is like a complex number with norm 1. This analogy works in regard to addition, multiplication, exponentiation, and adjoint (which is like complex conjugate). Also, this analogy is a good way to remember that the eigenvalues of a hermitian operator are real. Under this analogy, you can see that everything in is anti-hermitian. A hermitian term plus a non-hermitian term is non-hermitian, in the same way that a real number plus a non-real is non-real. Remember, hermitian is like real, anti-hermitian is like imaginary and unitary is like a complex number with norm 1. This analogy works in regard to addition, multiplication, exponentiation, and adjoint (which is like complex conjugate). Also, this analogy is a good way to remember that the eigenvalues of a hermitian operator are real. Under this analogy, you can see that everything in  is real except for the term with an is real except for the term with an 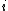 . The sum therefore is not hermitian (because it doesn't look like a real number). . The sum therefore is not hermitian (because it doesn't look like a real number).
I didn't really have time to look at the equation on question #100, so the way I got it was by seeing that since  lowered something (the energy) it was a ladder operator. Typically the "opposite" of a ladder operator is its adjoint so we have lowered something (the energy) it was a ladder operator. Typically the "opposite" of a ladder operator is its adjoint so we have 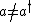 . This makes III true and II false (those two statements are exact opposites of each other). . This makes III true and II false (those two statements are exact opposites of each other).
 doesn't commute with doesn't commute with  because it changes the energy level so it is easy to see that because it changes the energy level so it is easy to see that 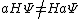 , since , since  "measures" the energy. "measures" the energy. |  | theevilmachines
2009-10-03 16:30:04 | This test was haaaaaaaaaaaaaaard
pam d
2011-09-21 19:08:56 |
a 67 raw score got you a 990
|
Setareh
2011-10-13 03:50:00 |
Oh yes! Really hard!
|
mpdude8
2012-04-20 19:40:54 |
Yeah, and a 56 was the 900 cutoff. Even if you only answered 75 questions and got 15 wrong, you'd still get a 900 on this test.
|
hjq1990
2012-10-14 06:06:07 |
Hey man, this is never easy, for time hardly allows careful consideration.
|
|  | CaspianXI
2009-04-03 14:40:12 | If you're fortunate enough to make it this far in the GRE, you're probably running very low on time. So, realize that I implies II -- that is, if an operator commutes with the Hamiltonian, it must be an observable. Also, if III is true, "a" is not an observable.
Hence, either both I and II are true, or III is true. We've eliminated everything except C and D. If you're concerned that time might be called any second, just guess. If you have a 30 seconds or more left, realize that the complex conjugate of "a" cannot equal "a". So, III must be true., Go with C.
echo
2009-09-24 23:33:52 |
There's one thing that bothers me. If you explicitly write 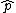 in the expression of in the expression of 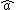 you get:rn you get:rn = \sqrt{\frac{m\omega_0}{2\hbar}}(\hat{x} + \frac{\hbar}{m\omega_0}\frac{\partial}{\partial x})) which is equal to its complex conjugate. So it seems like one should be mindful that the complex conjugate of a differential operator is not necessarily the same as the Hermitian conjugate of that operator. Things work out here because which is equal to its complex conjugate. So it seems like one should be mindful that the complex conjugate of a differential operator is not necessarily the same as the Hermitian conjugate of that operator. Things work out here because ^{\dagger} = -\frac{\partial}{\partial x}) . .
|
|  | physicsisgod
2008-11-07 14:44:21 | I think we can eliminate (II) because the eigenvalues of 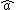 are definitely not observables. The index of the stationary state, n, is not a physical quantity. The trick to this problem, then, is eliminating (I), and I think evanb provides the best reason for that. are definitely not observables. The index of the stationary state, n, is not a physical quantity. The trick to this problem, then, is eliminating (I), and I think evanb provides the best reason for that. |  | phys2718
2008-10-14 10:28:48 | Formally if you take the commutator of  and the Hamiltonian, and the Hamiltonian, ![[x + ip, x^{2} + p^{2}]](/cgi-bin/mimetex.cgi?[x + ip, x^{2} + p^{2}]) , it is a relatively simple calculation to see that you don't get , it is a relatively simple calculation to see that you don't get 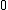 . . |  | sawtooth
2007-10-30 10:17:44 | Question: Why are we so sure to say 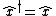 and more importantly and more importantly 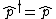 ? We all know that momentum and space are observables and so they have hermitian operators, but if you check, for the momentum we have: rnrn ? We all know that momentum and space are observables and so they have hermitian operators, but if you check, for the momentum we have: rnrn^\dagger = i\hbar \frac{d}{dx} = - \hat{p}) rnrnso the momentum operator is not hermitian. Ofcourse, with careful study, it turns out this is not the entirely correct way to take the adjoint, and the momentum operator is self-adjoint (hermitian) only with specific boundary conditions. So, my question is, do we assume these conditions hold in this harmonic oscillator problem (since we know it's an observable) and therefore we quickly get to the point where rnrnso the momentum operator is not hermitian. Ofcourse, with careful study, it turns out this is not the entirely correct way to take the adjoint, and the momentum operator is self-adjoint (hermitian) only with specific boundary conditions. So, my question is, do we assume these conditions hold in this harmonic oscillator problem (since we know it's an observable) and therefore we quickly get to the point where 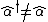 due to the minus before the momentum operator?rnrnFinally, I can add, if somenone doesn't recognise the ladder operator, I think they can reject I since we know that a conservable quantity commutes with the hamiltonian. Momentum is conserved, but there's no such law for space (in this context, at least i think) so the operator -related observable (which is the sum of the two) is not conserved and hence the operator doesn't commute with H. Correct me if I am wrong.rnrnAlso, correct me if I am wrong^2, but doesn;t the fact that due to the minus before the momentum operator?rnrnFinally, I can add, if somenone doesn't recognise the ladder operator, I think they can reject I since we know that a conservable quantity commutes with the hamiltonian. Momentum is conserved, but there's no such law for space (in this context, at least i think) so the operator -related observable (which is the sum of the two) is not conserved and hence the operator doesn't commute with H. Correct me if I am wrong.rnrnAlso, correct me if I am wrong^2, but doesn;t the fact that  and the hamiltonian have eigenvalues different in this way, mean that they don't commute? Wild guess, didnt think of it thoroughly. and the hamiltonian have eigenvalues different in this way, mean that they don't commute? Wild guess, didnt think of it thoroughly.
evanb
2008-07-03 14:25:31 |
p --absolutely must-- be self-adjoint, because it is observable. The only boundary conditions that we need to apply is that  is square-integrable (goes to zero quick enough that the boundary term is ignored), which holds true for a harmonic potential. From this, you can deduce that a is not hermitian, eliminated II. is square-integrable (goes to zero quick enough that the boundary term is ignored), which holds true for a harmonic potential. From this, you can deduce that a is not hermitian, eliminated II.
For the last piece, "doesn't the fact that a and the hamiltonian have different eigenvalues in this way mean that they don't commute?" That's a weirdly-phrased question, mainly because you don't explain what "this way" is supposed to mean. However, if you know that the eigenstates of the ladder operators are coherent states and the eigenstates of the hamiltonian are NOT coherent states (they are stationary states), that is enough to say that H and a do not commute, eliminating I and leaving (C) as the answer.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
