|
GR9277 #36
|
|
|
Problem
|
|
\prob{36}
A plane-polarized electromagnetic wave is incident normally on a flat, perfectly conducting surface. Upon reflection at the surface, which of the following is true?
- Both the electric vector and magnetic vector are reversed.
- Neither the electric vector nor the magnetic vector is reversed.
- The electric vector is reversed; the magnetic vector is not.
- The magnetic vector is reversed; the electric vector is not.
- The directions of the electric and magnetic vectors are interchanged.
|
Electromagnetism }Boundary Conditions
The conductor perfectly reflects the incoming wave, and none is transmitted. The electric field is thus reversed. However, since E and B are perpendicular (related to each other by the Poyting Vector where the direction of propagation is given by the direction of 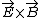 ), the magnitude of B is increased by 2, but its direction stays the same.
Search on the GRE Physics Solutions homepage with keyword conductors for more on this.
|
|
|
Alternate Solutions |
Herminso
2009-09-13 17:12:50 | By BC's the parallel components of the electric field at the conducting boundary need to be continuous. Since the wave is incident normally on a flat, we know that the electric and magnetic field of the electromagnetic wave are parallel to the surface (Remember 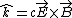 ). So the BC for the electric field is:
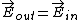
or
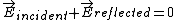
where 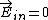 because the field inside to a conductor must be zero. Thus 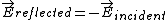 , the electric field is reversed.
Using now the relation 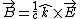 for the reflected wave, we can see the reflected magnetic field is not reversed.
|  |
|
|
Comments |
Herminso
2009-09-13 17:12:50 | By BC's the parallel components of the electric field at the conducting boundary need to be continuous. Since the wave is incident normally on a flat, we know that the electric and magnetic field of the electromagnetic wave are parallel to the surface (Remember 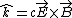). So the BC for the electric field is:
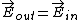
or
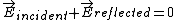
where 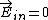because the field inside to a conductor must be zero. Thus 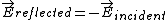, the electric field is reversed.
Using now the relation 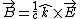for the reflected wave, we can see the reflected magnetic field is not reversed.
| | flux
2008-11-07 18:16:24 | Because the surface is a conductor, the E field must go to zero. This is similar to a rope with a fixed end. The E field will thus flip over and head the other direction. This leaves us with choices A and C. Using the right-hand-rule brings us to the conclusion that the B field holds its direction. Choice C it is! |  | Lukav
2008-10-03 12:42:32 | Kinda Silly, but you can just use the right hand rule to do this quickly.
Poop Loops
2008-10-05 15:38:38 |
Yes, but how do you know whether it's the E or B field that reversed?
|
| | Furious
2007-10-29 15:41:36 | This probably is stupid, but why is it that the transverse portion of the E field must be reversed, is this the same reason why two problems prior to this the transverse E field had to be zero? I'm not quite sure which physical concept is responsible for this.
nick1234
2007-10-29 17:41:14 |
There can't be an electric field along the surface of a conductor, otherwise the free electrons would move along the surface until the E-field was canceled. So, any E-field that exists must be perpendicular to the surface. (Griffiths p.98)
|
Poop Loops
2008-10-05 15:37:29 |
In short, yes, exactly that reason. E|| has to go to zero at the edges, whereas B|| can stay the same, so it makes sense that it would be E to flip directions.
|
| |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
|
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
|
