|
GR9277 #34
|
|
|
Problem
|
|
\prob{34}
A conudcting cavity is driven as an electromagnetic resonator. If perfect conductivity is assumed, the transverse and normal field components must obey which of the following conditions at the inner cavity walls?
-
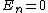 , , 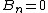
-
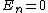 , , 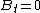
-
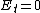 , , 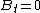
-
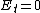 , , 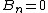
- None of the above
|
Electromagnetism }TEM Waves }TEM Waves
The full formalism of a conducting cavity can be solved via TEM (transverse electromagnetic) wave guides. However, to solve this problem, one needs only the two boundary conditions from the reflection at a conducting surface, 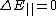 and and 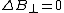 . .
The electric field parallel to the cavity is the transverse field, and thus one has choice (D), exactly the conditions above.
|
|
|
Alternate Solutions |
Daw6
2009-11-06 14:39:07 | I just thought about this question in terms of a plain old electromagnetic field in a cavity. If we just imagine some electromagnetic field source inside of an arbitrary enclosure, then only choice (D) makes sense;
E is a curl-less field (i.e. it only diverges), so for the E-field lines to be parallel with the inner walls of an enclosure is just silly.
B is a divergence-less field, (i.e. it only curls), so for the B-field lines to be perpendicular with the inner walls of the enclosure is equally as silly.
So only choice (D) makes sense. When you get down to it, it's really a very basic E+M question. |  |
|
|
Comments |
archard
2010-05-30 18:03:54 | Is it valid to solve this by thinking that the charges at the surface of the conductor must be stationary in order for the delicate arrangement of the charges to be such that the field inside remains 0? If that's the case then it's pretty obvious that the E field can't have a transverse component, because that would push charges along the surface. Likewise a normal B component would push the charges along the surface. |  | Daw6
2009-11-06 14:39:07 | I just thought about this question in terms of a plain old electromagnetic field in a cavity. If we just imagine some electromagnetic field source inside of an arbitrary enclosure, then only choice (D) makes sense;
E is a curl-less field (i.e. it only diverges), so for the E-field lines to be parallel with the inner walls of an enclosure is just silly.
B is a divergence-less field, (i.e. it only curls), so for the B-field lines to be perpendicular with the inner walls of the enclosure is equally as silly.
So only choice (D) makes sense. When you get down to it, it's really a very basic E+M question.
heypete
2010-11-05 16:12:03 |
That's a rather simple way of looking at it. I like it. Thanks.
|
|  | chrisfizzix
2008-10-06 12:16:10 | Conducting cavity = waveguide. You can find the first condition 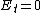 without knowing anything about waveguides by remembering that in a perfect conductor there can't be an electric field parallel to the surface. without knowing anything about waveguides by remembering that in a perfect conductor there can't be an electric field parallel to the surface. |  | sirius
2008-06-24 14:27:26 | i have never heard of conducting cavities, what topic is this from? is there a text i should look at for this?
Poop Loops
2008-10-05 15:22:16 |
Griffiths E&M covers it.
|
GREmania
2008-10-12 07:30:31 |
Looks like most of the problems are related to Griffiths Stuff.
|
|  | kevglynn
2006-09-25 12:28:15 | Could someone explain what a conducting cavity is (in general terms, an example of one, etc.)? Also, when it comes to the boundary conditions, what are the others?
Thanks
kevglynn
2006-10-15 19:16:01 |
nevermind, must have been groggy that morning. feel free to edit this out ;-)
p.s. Yosun is the man
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
