|
GR8677 #5
|
|
|
|
|
Alternate Solutions |
casseverhart13
2019-09-16 04:53:24 | Not too many people would actually think about this the way you just did. click here |  | archard
2010-08-04 14:05:45 | It's super easy if you write the kinetic energy as 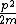 - since momentum is conserved, you don't even need to worry about whether or not the collision is elastic. - since momentum is conserved, you don't even need to worry about whether or not the collision is elastic.
Just write
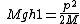
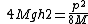
Divide equations and solve for h2. |  | PorcelainMouse
2008-11-05 15:12:32 | Thanks a19gray2. I completely forgot that. I was working this out and the three step process took me longer than I want. I think there is a quicker way. How about this?...
Recognize that the first and last steps are really the same: conservation of total energy, but where energy moves completely from potential to kinetic and back. For any complete conversion situation:
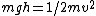
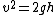
Right? So, now we know that
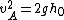 , ,
where 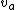 is the velocity of ball A and is the velocity of ball A and 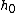 is it's initial height (where all of the E for this whole situation originates.) is it's initial height (where all of the E for this whole situation originates.)
And, we also know, from he same calculation, that
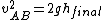 , ,
where 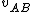 is the final velocity of both (stuck-together) balls and is the final velocity of both (stuck-together) balls and 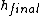 is their final height. is their final height.
We want to know the relation ship between 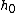 and and 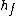 , so let's try this: , so let's try this:
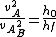
That's pretty close already. (And, you can see where the 1/16 comes from: it's the ratio of the squares of the velocity.) Now, since a19grey2 pointed out we need to use momentum to analyze the impact, we can write:
 v_{AB} )
But, now we only need to solve for 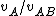 . .
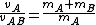
Let's square this, to match the ratio of squares we had relating the two heights:
^2 = \left(\frac{m_A + m_B}{m_A}\right)^2 )
Putting this last equation together with the previous ratio of velocities, we can find what we want:
^2 )
That makes 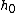 16 times as large as 16 times as large as 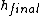 . Okay, it looks harder, but I think it's much faster because the algebra is quicker and easier. . Okay, it looks harder, but I think it's much faster because the algebra is quicker and easier. |  |
|
|
Comments |
casseverhart13
2019-09-16 04:53:24 | Not too many people would actually think about this the way you just did. click here |  | ernest21
2019-08-10 03:09:40 | The only variables/constants we can assume the units of are x and t. All others are unspecified, despite what convention suggests. artillery games |  | fredluis
2019-08-08 12:51:52 | It might be possible to do the derivation in a couple of minutes, if one is to know exactly what to look for. Consider the effective potential: tile contractor |  | joshuaprice153
2019-08-08 05:23:09 | That\'s a very good post, This post give truly quality information, I\'m definitely going to look into it, Really very useful tips are provided here, Thanks for sharing. commercial cleaning |  | archard
2010-08-04 14:05:45 | It's super easy if you write the kinetic energy as 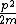 - since momentum is conserved, you don't even need to worry about whether or not the collision is elastic. - since momentum is conserved, you don't even need to worry about whether or not the collision is elastic.
Just write
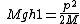
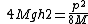
Divide equations and solve for h2.
flyboy621
2010-11-09 20:18:08 |
Nice!
|
timtammy
2011-10-11 00:57:49 |
far and away the best answer
|
Shahbaz Ahmed Chughtai
2012-06-09 22:45:14 |
Nice and Comprehensive Answer. :-)
|
|  | PorcelainMouse
2008-11-05 15:12:32 | Thanks a19gray2. I completely forgot that. I was working this out and the three step process took me longer than I want. I think there is a quicker way. How about this?...
Recognize that the first and last steps are really the same: conservation of total energy, but where energy moves completely from potential to kinetic and back. For any complete conversion situation:
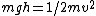
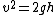
Right? So, now we know that
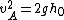 , ,
where 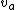 is the velocity of ball A and is the velocity of ball A and 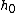 is it's initial height (where all of the E for this whole situation originates.) is it's initial height (where all of the E for this whole situation originates.)
And, we also know, from he same calculation, that
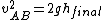 , ,
where 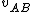 is the final velocity of both (stuck-together) balls and is the final velocity of both (stuck-together) balls and 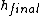 is their final height. is their final height.
We want to know the relation ship between 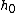 and and 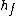 , so let's try this: , so let's try this:
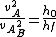
That's pretty close already. (And, you can see where the 1/16 comes from: it's the ratio of the squares of the velocity.) Now, since a19grey2 pointed out we need to use momentum to analyze the impact, we can write:
 v_{AB} )
But, now we only need to solve for 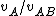 . .
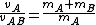
Let's square this, to match the ratio of squares we had relating the two heights:
^2 = \left(\frac{m_A + m_B}{m_A}\right)^2 )
Putting this last equation together with the previous ratio of velocities, we can find what we want:
^2 )
That makes 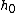 16 times as large as 16 times as large as 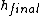 . Okay, it looks harder, but I think it's much faster because the algebra is quicker and easier. . Okay, it looks harder, but I think it's much faster because the algebra is quicker and easier.
nakib
2010-04-02 11:27:15 |
Thanks for the neat expression. Memorizing this will save me a minute in the exam for sure [assuming I get a similar kind of problem].
|
|  | Blake7
2007-09-11 18:30:50 | The bookkeeping is deceptively simple so get a good night's sleep and commit to the time expenditure in drudge cranking. |  | tercel
2006-12-01 11:18:28 | I'm confused. Why doesn't conservation of energy work to get directly from the initial condition to the solution?
In other words, where does the initial energy, 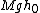 , go? , go?
VanishingHitchwriter
2006-12-01 14:10:43 |
Not sure if this is what you're asking, but the initial potential energy is converted to kinetic energy. However, when the two objects collide, momentum is transferred, and the velocity is changed (hence kinetic energy changed). The collision is completely inelastic (a la conservation of momentum).
|
a19grey2
2008-11-02 21:07:32 |
To clarify, ANY time that two objects stick together after a collison, energy is lost. Therefore, NEVER use conservation of energy to the before/after parts of a "stick together" collision.
|
flyboy621
2010-11-09 20:17:31 |
The energy lost in the collision typically goes into thermal energy, i.e. raising the temperature of the masses. Or it could go into vibrations or some other form of energy that does not contribute to translational motion.
|
|  | jax
2005-12-01 09:01:20 | It seems that only 19% of people got this one right, even though it seems easy. I guess most people probably assumed that the collision was elastic, which is not true. I messed up on that one too... ugh I hope I don't do something dumb like that on the exam! :)
dnvlgm
2007-11-11 19:22:58 |
well, it says the particles stick together, I guess most people read too fast or careless and that's a big problem that I honestly have a lot. Gotta be careful! Good luck with your exam!!! :D
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
