|
GR8677 #24
|
|
|
|
|
Alternate Solutions |
secretempire1
2013-03-18 10:58:28 | The easiest way I can think of is the following:
Look at the positive side of the generator, and the positive side of the battery. In between, there is a 20 V drop across two resistors.
Using Ohm's law, I = 10A = V/R = 20 V / 1+R.
Solve for R, it's that simple. |  |
|
|
Comments |
casseverhart13
2019-10-11 06:38:36 | Thanks, very nice problem. https://www.pressurewashingcapecoral.com |  | fredluis
2019-08-09 04:24:48 | Note that if the fields were perpendicular to each other the electron would drift in a helical pattern as in choice (C). tree removal |  | joshuaprice153
2019-08-09 01:54:59 | I’m happy I located this blog! From time to time, students want to cognitive the keys of productive literary essays composing. Your first-class knowledge about this good post can become a proper basis for such people. nice one! makeup artist Orlando |  | blacksheep
2017-09-21 23:33:20 | You certainly could do this using Kirchoff\'s Loop Rule, but I just took the approach you did of writing an equation based on what\'s happening. What\'s important to realize is that the battery in this problem is being *charged,* it is not a source of emf; the generator is the source. Thus the voltage drop due to the battery\'s internal resistance is added to the emf, as is the voltage drop across the resistor, all of which must be supplied by the generator. My equation looked like this: (100 volts) + (10 amps)(1 ohm) + (10 amps)(R) = 120 volts. Solve for R to get 1 ohm. |  | richard7893
2015-05-05 08:21:24 | Don't understand the R+1 part. Here's my loop:
-120V + (100V - 10A(1 ohm)) - 10A(R)=0
R=3 ohm , not a choice. Can someone let me know where I went wrong?
Jdogzz
2015-10-22 17:57:42 |
The problem there is that you assumed the direction of the current can be taken to flow \\\\\\\"positively\\\\\\\" no matter which way you apply the loop rule. Since the generator has the larger potential it controls the direction of the current, it must flow clockwise through the loop. So we can apply the loop rule two ways, traversing the loop clockwise or counterclockwise, and we can still subtract, as usual the potentials from components of resistance, but we will take the direction of the flow of current into account through the value of the current:\\\\r\\\\n\\\\r\\\\nMethod 1 (clockwise, so 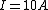 ):\\\\r\\\\n ):\\\\r\\\\n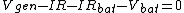 \\\\r\\\\n \\\\r\\\\n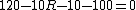 \\\\r\\\\n \\\\r\\\\n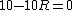 \\\\r\\\\n \\\\r\\\\n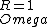 \\\\r\\\\n\\\\r\\\\nMethod 2 (counterclockwise, so \\\\r\\\\n\\\\r\\\\nMethod 2 (counterclockwise, so 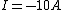 ) (this is the direction you initially used in your loop rule)\\\\r\\\\n ) (this is the direction you initially used in your loop rule)\\\\r\\\\n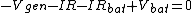 \\\\r\\\\n \\\\r\\\\n \\\\r\\\\n \\\\r\\\\n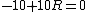 \\\\r\\\\n \\\\r\\\\n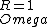 (the same as in method 1)\\\\r\\\\n\\\\r\\\\nIt is helpful to remember that when you do this the other way around, finding the current rather than having it provided and looking for something else), you can arbitrarily choose to do the loop rule clockwise or counterclockwise, you just have to check the resulting sign of the current at the end which tells you that you went the right way around if your answer was positive, and the opposite way if your answer was negative (though analysis ahead of time may be possible if you have a nice enough scenario where you can see which potential wins out).\\\\r\\\\n\\\\r\\\\nAlternatively, for those who would prefer not to give current a negative value, you may take the direction of the current into account by adding the potential contributions from resistances, instead of the usual subtraction, when you are crossing it opposing the flow of current as you are now acknowledging that you are going across a potential increase (so adding the potential contribution) rather than taking it at face value to be a potential decrease (subtracting the potential contribution) which you then correct later with the sign of the current:\\\\r\\\\n\\\\r\\\\nMethod 2 Alternative (counterclockwise, (the same as in method 1)\\\\r\\\\n\\\\r\\\\nIt is helpful to remember that when you do this the other way around, finding the current rather than having it provided and looking for something else), you can arbitrarily choose to do the loop rule clockwise or counterclockwise, you just have to check the resulting sign of the current at the end which tells you that you went the right way around if your answer was positive, and the opposite way if your answer was negative (though analysis ahead of time may be possible if you have a nice enough scenario where you can see which potential wins out).\\\\r\\\\n\\\\r\\\\nAlternatively, for those who would prefer not to give current a negative value, you may take the direction of the current into account by adding the potential contributions from resistances, instead of the usual subtraction, when you are crossing it opposing the flow of current as you are now acknowledging that you are going across a potential increase (so adding the potential contribution) rather than taking it at face value to be a potential decrease (subtracting the potential contribution) which you then correct later with the sign of the current:\\\\r\\\\n\\\\r\\\\nMethod 2 Alternative (counterclockwise, 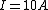 , but resistances now being added)\\\\r\\\\n , but resistances now being added)\\\\r\\\\n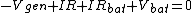 \\\\r\\\\n \\\\r\\\\n \\\\r\\\\n \\\\r\\\\n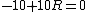 \\\\r\\\\n \\\\r\\\\n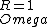
|
Jdogzz
2015-10-22 18:01:38 |
Apologies for the poor formatting, I have no idea why it went so horribly...
|
|  | secretempire1
2013-03-18 10:58:28 | The easiest way I can think of is the following:
Look at the positive side of the generator, and the positive side of the battery. In between, there is a 20 V drop across two resistors.
Using Ohm's law, I = 10A = V/R = 20 V / 1+R.
Solve for R, it's that simple. |  | pauria
2010-07-02 23:03:17 | Sorry, forgot to flag the below as typo. |  | pauria
2010-07-02 23:02:32 | I don't know what kind of arithmetic is going on here but the answer is R=1, not 1/2.
Just check the answer table at the top; it's C.
pam d
2011-09-23 20:57:55 |
Yosun has the answer as 1 ohm, that 1/2 you're seeing is just a 1 with capital omega.
|
|  | angiep
2005-11-11 14:32:45 | typo: I = 10 amperes
yosun
2005-11-11 20:39:02 |
angiep: thanks for the typo-alert; the typo has been corrected.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
