casseverhart13
2019-10-03 03:53:24 | I just intended to drop by but I ended up reading for hours, browsing for past entries. our site |  |
ernest21
2019-08-10 03:09:26 | I solved it using Maxwell\'s equations. The given equation is Ampere\'s law in differential form. planet coaster vr |  |
fredluis
2019-08-08 12:58:51 | This is a well-thought of piece that made it easy for people to understand the whole point. tile contractor |  |
joshuaprice153
2019-08-08 06:49:13 | This blog is very nice.I really like such a fantastic written blog.I will keep coming here again and again.Visit my link as well. tree pruning |  |
Jovensky
2013-01-13 20:19:54 | This is the way I understand this problem.
First, it is useful to have the interference equation to refer to:
I=I1+I2+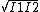 cos(phi) cos(phi)
where phi is the relative phase of the 2 waves.
Before the the phase is varied, the problem states that there is an interference pattern on the screen. The phase factor can depend on both position and time. If the interference factor only depends on position then the interference pattern is fixed in position on the screen. The phase can also be time dependent, where the interference pattern will shift on the screen, i.e if we look at one particular point on the screen that point will oscillate back and forth from constructive interference to destructive interference and back, how fast it oscillates depends on the phase frequency.
Now we add a relative phase that is time dependent. The addition of this has exactly the same effect as the time dependent part phase factor that I just mentioned. But in this case, the phase is varied very fast, it goes from 0 to 2pi 500 times a second, so the effect is undetectable by our eyes and we continue to see the original interference pattern on the screen.
A. Frequency of phase change affects how fast the interference pattern change. It is independent of the wavelength of the wave.
B. I don't think 500Hz is a multiple of pi anyway? But whether frequency of phase change is a multiple of pi or not does not matter.
C. When the total relative phase of the 2 waves is pi/2 or 3pi/2, there is no interference. At any other points there will be interference.
D. The monochromacity of light is not affected.
E. The correct answer as explained. |  |
nakib
2012-09-29 14:57:36 | (A) No. Change in coherence will affect interference.
(B) No. Same reason as in (A), also"frequency of of phase change" being multiple of  has nothing to do with interference. has nothing to do with interference.
(C) No. A phase change of  means that the waves are anti-phased. No question of interference here. means that the waves are anti-phased. No question of interference here.
(D) No. Phase change has nothing to do with monochromaticity.
(E) This must be it then. Also, although there are phase angles for which interference will occur but to a human eye there will appear none. The observer will conclude that the sources are incoherent.
nakib
2012-09-29 15:02:32 |
I take back the reason for elimination of (C). It should be eliminated because you can have interference for all possible phase differences. Sorry about that.
|
|  |
ph.samanta
2011-11-30 07:43:04 | I think relative phase change betn two waves can ordinarily be treated as phase change betn the two waves.phase changes occur 500 times from 0 to 2pi in 1sec,the fringe pattern shift very rapidly.i.e E will be correct. |  |
bingsong
2010-02-26 04:09:37 | B
pam d
2011-09-23 19:53:40 |
No. The answer is (E).
|
|  |
glkjap
2008-05-04 14:23:09 | You said: "Interference is produced as long as the sources are coherent, and the sources are coherent as long as there's a constant relation between relative phase in time."
But the sources don't have a constant phase. It changes from 0 to 2 , right? So how are they coherent? , right? So how are they coherent?
dean
2008-10-09 20:11:29 |
There are degrees of coherence, and the difference between frequencies of 10^2 and 10^14 is great enough that we can say the beams are still coherent. The light sources are at pretty much the same phase for many wavelengths.
|
|  |
