|
GR0177 #30
|
|
|
Problem
|
|
|
This problem is still being typed. |
Atomic }Hydrogen Atom }Hydrogen Atom
The hydrogen atom wave-functions all have to do with an exponentially decreasing radial function. Thus, choose choice A. (FYI: Only the spherical harmonic angular parts have trig involved, and thus choice.)
|
|
|
Alternate Solutions |
flyboy621
2010-11-16 21:01:03 | A couple of people have mentioned it below, but it's worth putting up top: the reason III doesn't work is because it's not normalizable when squared and integrated over all space.
It doesn't matter that the function blows up at zero, because when you integrate, a factor of r^2 comes in. That keeps the probability density finite, which is OK. The problem is that the probability density does not vanish at infinity. |  | saberbud
2010-11-09 06:01:14 | Integrate the wave function:  psi^2 *4pi *r^2*dr psi^2 *4pi *r^2*dr
"II" obviously would not converge, therefore, can't be normalized.
This is the true reason. |  | vroomfondel
2006-12-01 01:16:43 | A/r blows up at 0
ASin(br) does not go to 0 at infinity
only 1 satisfies both. |  | scottopoly
2006-10-29 22:14:45 | I think the only way to very correctly say that "I" is the only correct one is to realize two facts: the solution from the QM problem is a decaying exponential (you would need this memorized I think), exponentials do not form a complete set of functions, so you cannot build other functions from them (choice II and III are wrong then)
Let me know if I am correct here. |  |
|
|
Comments |
scrabble
2011-03-11 10:51:29 | As mentioned before, both II and III are not possible because they are not square-integrable. "Blowing up" at some point is not a criterion: Since we are only interested in integrals over the square of the wavefunction, in general 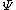 can do a lot of crazy stuff, including having singularities and being discontinuous. can do a lot of crazy stuff, including having singularities and being discontinuous.
Anyway, here's another way to look at it:
Just look at the Schrödinger equation - you don't have to solve it, but it's always good to deduce some facts about the shape of the wave function.
We know that the second derivative of the wave function is only zero at one single point: At the point where the energy E (which is negative for a bounded electron) intersects with the potential 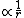 , the wavefunction will have an inflection point. Therefore, II can be ruled out, because it is obviously periodic and has an infinite number of inflection points. , the wavefunction will have an inflection point. Therefore, II can be ruled out, because it is obviously periodic and has an infinite number of inflection points.
III can be ruled out in the same way, since it has no turning point.
FutureDrSteve
2011-11-07 12:34:59 |
I was under the impression that the wave function is always continuous. Maybe it's just the time-independent wave function that's always continuous. Isn't that what we're dealing with here? Please, someone let me know if I'm off base.
|
|  | flyboy621
2010-11-16 21:01:03 | A couple of people have mentioned it below, but it's worth putting up top: the reason III doesn't work is because it's not normalizable when squared and integrated over all space.
It doesn't matter that the function blows up at zero, because when you integrate, a factor of r^2 comes in. That keeps the probability density finite, which is OK. The problem is that the probability density does not vanish at infinity. |  | saberbud
2010-11-09 06:01:14 | Integrate the wave function:  psi^2 *4pi *r^2*dr psi^2 *4pi *r^2*dr
"II" obviously would not converge, therefore, can't be normalized.
This is the true reason.
saberbud
2010-11-09 06:02:29 |
Sorry, I mean III is not reasonable.
II is too obvious to be explained.
|
saberbud
2010-11-09 06:03:02 |
I mean"III", this is a typo.
|
|  | saberbud
2010-11-09 06:00:12 | Integrate the wave function: psi^2 *4pi *r^2*dr
"II" obviously would not converge, therefore, can't be normalized.
This is the true reason. |  | eliasds
2008-09-20 14:49:28 | Choice II DOES work iif you choose A and b to be imaginary numbers. What do you all say to that!?!?
a19grey2
2008-11-05 21:51:43 |
ETS doesn't use imaginary numbers on this test unless they are very explicit about it.
|
|  | DanS510
2008-09-20 14:47:05 | Choice II DOES work iif you choose A and b to be imaginary numbers. What do you all say to that!?!? |  | Furious
2007-10-19 18:34:03 | I'm not sure if people are even still checking. But wouldn't the function blowing up at zero be a good reason for thinking its a wave function?
I mean I thought as r goes to zero we get hardshell repulsion, and that it's physically impossible for the electron to be in the very center of the nucleus, hence it blowing up as r -> 0.
But I mean, I have the solutions right here, and it says that its only A. I'd like to know why that rationale is wrong.
Gaffer
2007-10-20 12:00:11 |
Since the wave function squared is associated with the probability of finding a particle at some location x, blowing up at zero is bad. An infinite value for the wave function implies that there is an "infinite" probability of the particle being at that location, it throws off all the other finite location values- ie, for 1/r, the electron couldn't be ANYWHERE except at the middle of the nucleus, which is obviously untrue.
The decaying exponential fits the bill since it has a finite value at r = 0 (so the probability distribution is normalizable) and probability goes to 0 for large r. Non-normalization is also why the sin(r) form does not follow. r is unrestricted and so the sin just keeps oscillating. With the angular functions, you limit your variable to pi etc. not all angles and you can normalize you probability.
|
greed
2008-08-24 15:57:35 |
As far as I know, wave functions that blow up a the origin are fine provided that they are square-integrable. You could have /r^2) which is divergent at which is divergent at 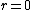 but but 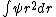 is finite is finite
|
|  | vroomfondel
2006-12-01 01:16:43 | A/r blows up at 0
ASin(br) does not go to 0 at infinity
only 1 satisfies both. |  | scottopoly
2006-10-29 22:14:45 | I think the only way to very correctly say that "I" is the only correct one is to realize two facts: the solution from the QM problem is a decaying exponential (you would need this memorized I think), exponentials do not form a complete set of functions, so you cannot build other functions from them (choice II and III are wrong then)
Let me know if I am correct here.
Walter
2008-08-12 16:47:49 |
The question does not say that the wavefunction is for a hydrogen atom, just "an electron in an atom", so the inference that just because the hydrogen radial wavefunctions have a decaying exponential then the decaying exponential answer is the only correct answer is a bad inference. It could be a multielectron atom or whatever.
This idea about 'complete set of functions' is way off as well. In the case of finding an analytical solution to the differential equation then any damn function will do, it doesn't have to be something like a trig function or complex exponential that you can use to generate infinite series to represent arbitrary other functions.
The vroomfondel solution is correct for the reasons given.
|
|  | tera
2006-09-13 13:46:14 | But A/r disappears in infinity there so why it is not the correct answer?
askewchan
2008-11-07 15:17:25 |
Because as 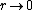 we have we have 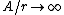 . The electron can't have an infinite wave function at the center of the nucleus. . The electron can't have an infinite wave function at the center of the nucleus.
|
Phobos
2010-09-13 11:54:14 |
 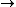  at r=0 was not so suspicious to me. But this wavefunction is clearly illegal because its integral over space diverges. Integrating over spherical coordinates introduces an at r=0 was not so suspicious to me. But this wavefunction is clearly illegal because its integral over space diverges. Integrating over spherical coordinates introduces an 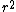 , and the integrand is a constant. , and the integrand is a constant.
|
|  | keflavich
2005-11-10 11:47:48 | It looks like you stopped before the end of the sentence here. Choice II doesn't work because it's a spherical harmonic, not a radial WF. You could also eliminate II and III by taking the limit as r-> and realizing the WF must disappear out there. and realizing the WF must disappear out there. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
