|
|
|
| All Solutions of Type: Electromagnetism | | 3 | Click here to jump to the problem! | GR8677 #11
|
Electromagnetism }Vector Calculus }Vector Calculus
There are two identities from vector calculus one has to know by heart. The one directly applicable to this problem is:
=0<br />
)
Plug in the equation given in the problem to the identity above to get 0.
(The other identity, not quite as useful for this problem, but perhaps useful for subsequent problems, is: ) ) )
|
| 4 | Click here to jump to the problem! | GR8677 #22
|
Electromagnetism }Lorentz Transformation }Lorentz Transformation
When an electric field is Lorentz-transformed, afterwards, there might be both a magnetic and electric field (in transverse components). Or, more rigorously, one has,
\\
E_z'&=& \gamma(E_z+vB_y)\\
B_x' &=& B_x\\
B_y' &=& \gamma(B_y + E_z v/c^2)\\
B_z' &=& \gamma(B_z-vE_y/c^2),<br />
\end{eqnarray})
for motion in the  direction. direction.
(A) Obviously not. Suppose initially, one has just 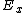 , afterwards, there's still , afterwards, there's still 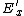 . .
(B) True, as can be seen from the equations above.
(C) Not true in general. Suppose 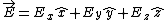 . Afterwards, the transverse components are off by a . Afterwards, the transverse components are off by a 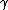 even if there's no B field to start with. even if there's no B field to start with.
(D) Nope.
(E) Mmmm... no need for gauge transformations.
|
| 7 | Click here to jump to the problem! | GR8677 #29
|
Electromagnetism }Right Hand Rule }Right Hand Rule
Note: this is a negative test charge. So, for the test charge, one has to either choose the opposite direction as that yielded by the Right Hand Rule or one could use the Left Hand Rule, which is just the RHR done with the left hand.
Suppose the current is a straight line pointing upwards along the page. The RHR for the current shows a magnetic field that's coming out of the page from the left side of the current and a field going into the page on the right side.
The problem wants the test charge to go parallel to the current. Applying the Lorentz Force, where 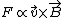 , one finds that no matter the direction of approach, the only way for the force to point parallel to the current is for the velocity to go towards the wire. (Check this: Suppose the charge comes in from the left; the force would point parallel to the current. Suppose the charge comes in from the right; the force would point parallel to the current, again.) , one finds that no matter the direction of approach, the only way for the force to point parallel to the current is for the velocity to go towards the wire. (Check this: Suppose the charge comes in from the left; the force would point parallel to the current. Suppose the charge comes in from the right; the force would point parallel to the current, again.)
|
| 9 | Click here to jump to the problem! | GR8677 #53
|
Electromagnetism }Accelerating Charges }Accelerating Charges
One doesn't really need to understand the mess Griffiths has on accelerating charges to solve this problem. In fact, common sense works. Since the particle spends the most time about the origin, the field there should be maximal. The origin corresponds to 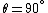 , via the system used in the diagram. This is choice (C). , via the system used in the diagram. This is choice (C).
|
| 10 | Click here to jump to the problem! | GR8677 #54
|
Electromagnetism }Dielectric }Dielectric
Recall the following equations,
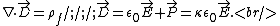
Also, recall the relation between bound charge and polarization,
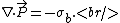
Use the divergence theorem on the above equations to apply the elementary Gauss' Law to the region,


But, since 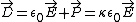 , one has , one has 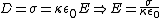 . Plug that into the other relation for D (and use the result for P from above) to get, . Plug that into the other relation for D (and use the result for P from above) to get, 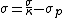 . Thus, . Thus, 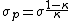 , as in choice (E). , as in choice (E).
|
| 11 | Click here to jump to the problem! | GR8677 #63
|
Electromagnetism }Method of Image Charge }Method of Image Charge
The boundary condition at the conducting plane is =0) . This doesn't mean that one can't put an ``image charge" a distance . This doesn't mean that one can't put an ``image charge" a distance 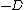 away on the other side of the plane to make the calculation easier. Making the directest straight line from the charge to the plane along the away on the other side of the plane to make the calculation easier. Making the directest straight line from the charge to the plane along the  axis, one gets the following image-charge potential: axis, one gets the following image-charge potential:
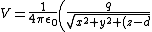^2}}-\frac{q}{\sqrt{x^2+y^2+(z+d)^2}}\right).<br />
)
The charge density for a grounded conducting plane is given by 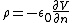 , where , where  is the direction of the directest straight line. The derivative is, is the direction of the directest straight line. The derivative is,
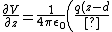}{\left(x^2+y^2+(z-d)^2\right)^1.5}-\frac{q(z+d)}{\left(x^2+y^2+(z+d)^2\right)^{1.5}}\right),<br />
)
and thus, after combining terms, the density is
^2\right)^{1.5}}
)
The problem wants the surface charge density a distance  away from the point charge. So, plug in away from the point charge. So, plug in ^2\right)^{1.5}=(D^2)^{1.5}) to get to get
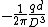
|
| 13 | Click here to jump to the problem! | GR8677 #65
|
Electromagnetism }Biot-Savart Law }Biot-Savart Law
One either remembers the field of a circular current loop or one derives it from the Bigot-Savart Law,
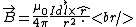
One finds that 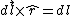 , as they're perpendicular. , as they're perpendicular. 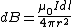 , and the vertical components of the field cancel, thus there are only the horizontal components (parallel to the axis of the ring). , and the vertical components of the field cancel, thus there are only the horizontal components (parallel to the axis of the ring).  is the directest distance from a differential element on the wire to a point on the axis, and is the directest distance from a differential element on the wire to a point on the axis, and  is the horizontal distance (along the axis) from the center of the ring to that point. Thus, the integral becomes, is the horizontal distance (along the axis) from the center of the ring to that point. Thus, the integral becomes,
^{3/2}} = \frac{\mu_0 I b}{2 }\frac{b}{(x^2+b^2)^{3/2}}, <br />
)
where 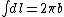 . .
So anyway, the field, at a point anywhere along the axis of the loop is 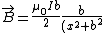^{3/2}}) . .
At a point far, far, away, 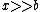 , and thus , and thus 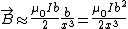 . .
Set  , where , where  is the fixed coordinate of that point, to get that the field is proportional to is the fixed coordinate of that point, to get that the field is proportional to 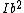 . .
Incidentally, defining the magnetic dipole moment to be 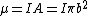 , one finds the field of a magnetic dipole to be , one finds the field of a magnetic dipole to be 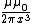 . The field far from a current loop is the same as the field of a magnetic dipole. . The field far from a current loop is the same as the field of a magnetic dipole. |
| 17 | Click here to jump to the problem! | GR8677 #86
|
Electromagnetism }Coulomb's Law }Coulomb's Law
(Better classified as the Cavendish-Maxwell Experiment to determine the exponent in Coulomb's Law.)
One wonders why the common sense (and much too trivial) answer, choice (D), isn't right. In searching through one's lower level textbook, one would find accounts of Cavendish's Torsion experiment, which seems to also support choice (D). However, reading up on papers, one finds that the precise determination of the exponent is actually done via a whole different method... which although is an experimental technique, actually serves to illuminate the necessity of the inverse square law---and thus, this problem is not classified as a Lab Technique problem.
Charge up a conducting shell. Put a charge inside, distinctly asymmetrically far from the center but not touching the outer shell. One finds that the charge will not move.
This suggests that the field is 0.
Suppose that the field contribution to the test charge can be broken down into two unequal parts, set apart by a plane through the test-charge. 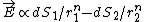 . Substituting the solid angle . Substituting the solid angle 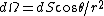 , one finds that , one finds that ) . Since the field vanishes for any . Since the field vanishes for any 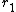 , , 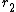 , one deduces that , one deduces that 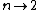 . .
For other and more modern methods, see page 95ff, especially page 100 of 
|
| 18 | Click here to jump to the problem! | GR8677 #94
|
Electromagnetism }LR Circuit }LR Circuit
Once the switch S is closed, although the initial current through the inductor is 0, the change in current through it is maximal. Recalling that 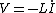 , one realizes that the voltage across , one realizes that the voltage across 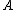 must be non-zero at the start. Thus, plots (C), (D), and (E) are eliminated. must be non-zero at the start. Thus, plots (C), (D), and (E) are eliminated.
Now, one must decide between choices (A) and (B). Once the circuit reaches equilibrium, i.e., the elements reach their asymptotic values. Specifically, the voltage at A goes to 0, since the inductor has no potential difference across it (to wit 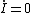 ). Once the switch is opened, the current suddenly changes, and ). Once the switch is opened, the current suddenly changes, and 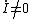 , thus the inductor has a voltage across it, and the voltage at A becomes nonzero. Because of the diode, this would necessarily have to be a negative voltage. Since there is only , thus the inductor has a voltage across it, and the voltage at A becomes nonzero. Because of the diode, this would necessarily have to be a negative voltage. Since there is only 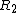 to dissipate the voltage, the magnitude of the voltage once the switch is opened should be bigger than that initially, when the switch is closed at to dissipate the voltage, the magnitude of the voltage once the switch is opened should be bigger than that initially, when the switch is closed at 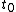 . Choose (B). . Choose (B).
|
| 20 | Click here to jump to the problem! | GR8677 #1
|
Electromagnetism }RC Circuit }RC Circuit
One can immediately eliminate plots A, C, E, since one would expect an exponential decay behavior for current once the switch is flipped.
More rigorously, the initial circuit with the switch 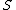 connected to connected to  has the following equation, has the following equation,
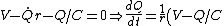<br />
)
Once integrated, the equation becomes,
<br />
)
The charge stored on the capacitor after it is fully charged is  (at (at 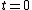 ). ).
When the switch 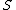 is switched to is switched to 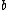 , the equation becomes, , the equation becomes,
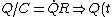 = Q_0 e^{-\frac{t}{RC}},<br />
)
where 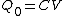 from the initial connection. from the initial connection.
Current is the negative time derivative of charge, and thus,
=-\dot{Q}=\frac{Q_0}{RC} Q(t) = \frac{V}{R}Q(t)<br />
)
The initial current IS =V/R) , and thus choice (B) is right. , and thus choice (B) is right.
|
| 26 | Click here to jump to the problem! | GR8677 #25
|
Electromagnetism }Capacitors }Capacitors
Recall the following truths (held to be self-evident?) on the subject of capacitors: 1. series capacitors have equal charge (Equivalent capacitance of two capacitors is 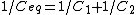 ); 2. parallel capacitance have equal voltage ( ); 2. parallel capacitance have equal voltage (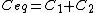 ); 3. ); 3.  ; 4. ; 4. 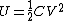 . .
(A) Initially, before the switch is closed, only 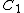 has a voltage across it, and hence it is charged. has a voltage across it, and hence it is charged. 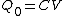 . But, afterwards, since the voltage stays the same, one has . But, afterwards, since the voltage stays the same, one has 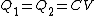 ; hence, ; hence, 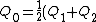) . .
(B) 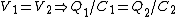 . Since . Since 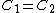 , one has , one has 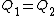 . This is true. . This is true.
(C) By definition of circuit elements in parallel, one has each capacitor at the same potential. This is trivially true. 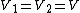
(D) Since one determined from (C) that the capacitors are at the same voltage, then because they have the same capacitance, they have the same energy as per 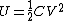 . True. . True.
(E) This is false, since 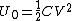 , initially. In the final state, each capacitor has energy , initially. In the final state, each capacitor has energy 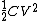 . The sum of energies is thus . The sum of energies is thus 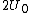 . .
|
| 30 | Click here to jump to the problem! | GR8677 #47
|
Electromagnetism }Faraday Law }Faraday Law
Recall Faraday's Law, 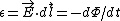 , where , where 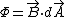 . In words, this means that a changing flux (either a varying field or radius) induces a voltage. . In words, this means that a changing flux (either a varying field or radius) induces a voltage.
The field is given as just B. The area of the loop is just 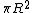 , i.e., the cross-sectional area of the cylinder. As the cylinder is spun around, its flux changes at the rate of N rps. The change in flux is thus , i.e., the cross-sectional area of the cylinder. As the cylinder is spun around, its flux changes at the rate of N rps. The change in flux is thus  , and this is the magnitude of the potential difference in choice (C). , and this is the magnitude of the potential difference in choice (C).
(Also, one can drop out the other choices from units. And, since the cylinder is moving in a magnetic field, the non-zero flux demands a voltage, so (A) can't be it.)
|
| 33 | Click here to jump to the problem! | GR8677 #62
|
Electromagnetism }Capacitors }Capacitors
 Initially, one has the two capacitors connected in parallel, so that each receives the same voltage from the battery. Thus
Initially, one has the two capacitors connected in parallel, so that each receives the same voltage from the battery. Thus 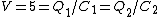 . . 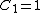 and and  , thus , thus 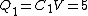 and and 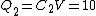 . .
After the battery is removed and the capacitors are re-connected so that the opposite plates face each other, one has (immediately) 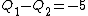 . The charges would then redistribute themselves so that the voltage across each capacitor is the same. Thus, denoting the final charge on each capacitor as . The charges would then redistribute themselves so that the voltage across each capacitor is the same. Thus, denoting the final charge on each capacitor as 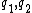 , respectively, one has (from charge conservation) , respectively, one has (from charge conservation) 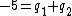 . Applying the equi-voltage condition, one has . Applying the equi-voltage condition, one has  . Plug that into the charge conservation equation to get . Plug that into the charge conservation equation to get 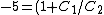q_2\Rightarrow q_2=3.33 \Rightarrow V=q_2/C_2 \approx 1.7) , as in choice (C). (As an exercise, one can also check by computing the charge for the other capacitor.) , as in choice (C). (As an exercise, one can also check by computing the charge for the other capacitor.)
|
| 34 | Click here to jump to the problem! | GR8677 #69
|
Electromagnetism }Ampere Law }Ampere Law
Recall Ampere's Law, 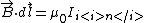 . .
Since the region one is interested in is a vacuum, one's Ampere Loop encloses all of the current. Thus, the field from each conductor is  = \mu_0 J \pi R^2) , where, , where, 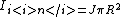 and R is the radius of the conductor. (This is a good approximation of the current, as one assumes that the vacuum region in the center is small compared to the area of the conductors.) and R is the radius of the conductor. (This is a good approximation of the current, as one assumes that the vacuum region in the center is small compared to the area of the conductors.)
Making the approximation that 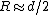 , one has , one has 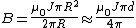 . Since both fields contribute in the center, the field is twice that, . Since both fields contribute in the center, the field is twice that, 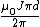 , as in choice (A). , as in choice (A).
(Also, one can immediately eliminate all but choices (A) and (B) by the right-hand rule. One seeks a +y-direction field.)
|
| 37 | Click here to jump to the problem! | GR8677 #86
|
Electromagnetism }Particle Trajectory }Particle Trajectory
There is a force pointing upwards from the Electric field in the y-direction. Suppose the particle is initially moving upwards. Then, the magnetic field would deflect it towards the right... One can apply the Lorentz Force to solve this problem.
If the particle comes in from the left, then the magnetic force would initially deflect it downwards, while the electric force would always force it upwards. Continue applying this analysis to each diagram. It turns out that one has cycloid motion whenever the electric and magnetic fields are perpendicular.
|
| 38 | Click here to jump to the problem! | GR8677 #87
|
Electromagnetism }Faraday Law }Faraday Law
From Faraday's Law or Len's Law, one has 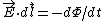 . Since, in order for the balls to move, they must move in a circle, one has . Since, in order for the balls to move, they must move in a circle, one has 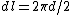 ; moreover, the induced magnetic field would point in the opposite direction to the field that was before, and one has a current in a loop from the right-hand-rule. The area of the magnetic flux is just ; moreover, the induced magnetic field would point in the opposite direction to the field that was before, and one has a current in a loop from the right-hand-rule. The area of the magnetic flux is just 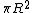 , since the field only goes through the cylindrical region of radius R. , since the field only goes through the cylindrical region of radius R.
Thus,  = \dot{B}\pi R^2 \Rightarrow E=\frac{\dot{B}R^2}{d}) . .
Now, recall some mechanics. The torque is related to the moment-arm and force by 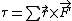 , where , where 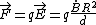 . Since there is a force contribution from each charge, and since, by the right-hand-rule, their cross-products with the moment-arm point in the same direction, one finds the torque to be . Since there is a force contribution from each charge, and since, by the right-hand-rule, their cross-products with the moment-arm point in the same direction, one finds the torque to be 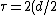q\frac{\dot{B}R^2}{d} = dq\frac{\dot{B}R^2}{d}=q\dot{B}R^2) . .
Now, recall the relation between angular momentum and torque to be  . Replace the . Replace the 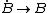 above to get above to get 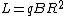 , and so the system starts rotating with angular momentum as in choice (A). (This approach is due to Matt Krems.) , and so the system starts rotating with angular momentum as in choice (A). (This approach is due to Matt Krems.)
Note that one can immediately eliminate choice (D) since angular momentum is not conserved from the external torque induced (to wit: electromagnetic induction). Moreover, although choice (E) is true in general, it does not apply to this problem.
|
| 41 | Click here to jump to the problem! | GR8677 #7
|
Electromagnetism }Field Lines }Field Lines
Since one has same polarity magnet ends at the same side, one can immediately cancel out choices (A) and (D). They would repel each other, and thus the field-lines would not be pointing towards each other. Since there are no such things as magnetic monopoles, one cannot have choice (C), as that would imply a non-zero divergence in the magnetic field. Choice (D) would work if there were a current through the magnets, but there's not. Choice (B) remains. It makes sense since the magnetic charges should repel each other, and thus the field lines should point away showing the repulsion.
|
| 42 | Click here to jump to the problem! | GR8677 #8
|
Electromagnetism }Conductors }Conductors
A conductor has the magical mystical property of inducing the exact opposite charge of a nearby charge. One has all the electrons in the conductor moving towards the positive charge placed outside Q. A net negative charge of -Q is induced.
(Also, one recalls that this was the assumption made in finding the potential of this setup using the Method of Images---the charged plane was assumed to have a charge density 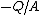 .) .)
|
| 43 | Click here to jump to the problem! | GR8677 #9
|
Electromagnetism }Electric Field }Electric Field
From symmetry, one has 0-field at the center. This is choice (A).
Take the limit of an infinite number of charges placed around the center. In two dimensions, one has a circle of charges. This is similar to a 2-dimensional conductor. There is 0-electric-field inside a conductor (the potential is constant inside). But, for a less-than-infinite number of charges, one would only have 0-field in the center. Gauss' Law inside would have a gaussian surface (just a loop in 2-dimensions) surrounding 0 charge.
The brute-force way would be to compute the electric field via Coulomb's Law and vector addition. With the proper coordinates and a 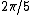 angle unit circle, this is a easy calculation. angle unit circle, this is a easy calculation.
|
| 45 | Click here to jump to the problem! | GR8677 #20
|
Electromagnetism }Bremsstrahlung }Bremsstrahlung
One might recall the English translation of Bremsstrahlung, which is "braking radiation." The only choice that has to do with acceleration is choice (E).
|
| 46 | Click here to jump to the problem! | GR8677 #38
|
Electromagnetism }AC Circuit }AC Circuit
The current is maximized when one has resonance. Resonance occurs when the complex impedance is 0, or when 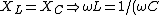) . Plug stuff in to get choice (D). . Plug stuff in to get choice (D).
|
| 47 | Click here to jump to the problem! | GR8677 #39
|
Electromagnetism }Filters }Filters
High-pass filters have, for high-frequencies (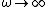 ), ),  . .
The net impedance is given by 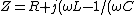)) . . 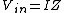 , and thus , and thus 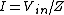 . .
For cases I and II, 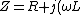) . .
For case I: 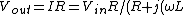)) Thus, in the regime of high, frequency, one gets Thus, in the regime of high, frequency, one gets 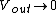 (This is a low-pass filter.) (This is a low-pass filter.)
For case II: 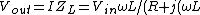)) , one gets , one gets  (To wit: L'Hopital's Rule can be used or this limit.) (To wit: L'Hopital's Rule can be used or this limit.)
For cases IV and III, )) . .
For Case III, ))) For high-frequency, For high-frequency,  \rightarrow 0) , and thus one has , and thus one has  . .
For Case IV, 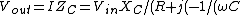))) . This quantity goes to 0 for high-frequency. (This is a low-pass filter.) . This quantity goes to 0 for high-frequency. (This is a low-pass filter.)
Hence, the only choices that work for high-freq filters are choices II and III. Choice (D).
|
| 49 | Click here to jump to the problem! | GR8677 #41
|
Electromagnetism }Monopoles }Monopoles
Theorists like monopoles because if they exist, Maxwell's equation would be symmetrical. Thus, one would get to add terms to the divergence of B and the curl of E to make it symmetric with their other-field counterparts. Choose choice (E).
|
| 50 | Click here to jump to the problem! | GR8677 #42
|
Electromagnetism }Faraday Law }Faraday Law
Faraday's law suggests that the current inducted opposes the changing field. (This is also known as Lenz Law). It acts something like an electromagnetic inertia.
Since the middle loop is moving towards the observer, the loop A feels an increasing current. Loop A will thus compensate with a current that acts to decrease the field-change; this current is counter-clockwise by the right-hand rule.
Since the middle loop is moving away from loop B, loop B will want to increase its magnetic field, and thus its current is in the same direction as the middle loop.
Only choice (C) works.
(One can immediately cancel out all but choices (A) and (B) from just a conceptual understanding of Lenz Law.)
|
| 54 | Click here to jump to the problem! | GR8677 #61
|
Electromagnetism }Boundary Conditions }Boundary Conditions
For a conductor, the electric field boundary condition at the interface are 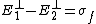 ( (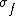 is the free charge density) and is the free charge density) and 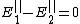 . .
The plane wave traveling in the x-direction is polarized (say) in the +z-direction. Thus, 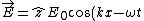) . .
There is no component perpendicular to the conductor at the boundary, and thus the first boundary condition implies that the free charge density is 0.
The second boundary condition requires that 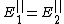 . The parallel component of E is polarized in the z-direction, and thus the requirement is . The parallel component of E is polarized in the z-direction, and thus the requirement is  , i.e., the incident plus the reflected is equal to the transmitted wave. However, for a perfect conductor, the transmitted wave is 0. Thus, one has , i.e., the incident plus the reflected is equal to the transmitted wave. However, for a perfect conductor, the transmitted wave is 0. Thus, one has 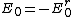 . This implies that the electric field to the left of the conductor cancels. . This implies that the electric field to the left of the conductor cancels.
Recall the Poynting vector,  , which conveniently points in the direction of the electromagnetic wave propagation. Since the electric field (by the convention used above) is polarized in the z-direction, the magnetic field of the incident wave points in the -y direction. However, since the electric field of the reflecting wave points in the -z-direction, its magnetic field also points in the -y direction. The magnetic field magnitude is thus , which conveniently points in the direction of the electromagnetic wave propagation. Since the electric field (by the convention used above) is polarized in the z-direction, the magnetic field of the incident wave points in the -y direction. However, since the electric field of the reflecting wave points in the -z-direction, its magnetic field also points in the -y direction. The magnetic field magnitude is thus 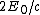 . Hence, one has choice (C). . Hence, one has choice (C).
|
| 60 | Click here to jump to the problem! | GR8677 #96
|
Electromagnetism }Symmetry }Symmetry
By symmetry, the total power radiated is 0. It expands inwards and outwards at the same frequency.
|
| 61 | Click here to jump to the problem! | GR8677 #9
|
Electromagnetism }Current Directions }Current Directions
The opposite currents cancel each other, and thus the induction (and field) outside is 0.
|
| 62 | Click here to jump to the problem! | GR8677 #10
|
Electromagnetism }Image Charges }Image Charges
The conductor induces image charges -q and -2q since it is grounded at 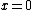 . Since these are (mirror) image charges, each charge induced is the same distance from the conducting plane as its positive component. . Since these are (mirror) image charges, each charge induced is the same distance from the conducting plane as its positive component.
The net force on q is just the magnitude sum of the positive charge 2q and the two induced charges, 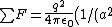 + 2/(2a^2) + 2/(a^2) \right) = \frac{q^2}{4\pi\epsilon_0a^2}\left( 1+1/2+2 \right) = \frac{q^2}{4\pi\epsilon_0a^2}\frac{7}{2}) , as in choice (E). , as in choice (E).
(Why is it the magnitude sum? Well, recall that 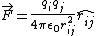 , where , where 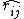 is the vector pointing from the charge one is interested in to the field charge, i.e., the other charge. If one has two positive charges, then the force points along that unit vector. However, if one has a minus charge and a positive charge, the force points in the other direction. Thus, all the force quantities are additive, and one might as well just take the magnitude sum.) is the vector pointing from the charge one is interested in to the field charge, i.e., the other charge. If one has two positive charges, then the force points along that unit vector. However, if one has a minus charge and a positive charge, the force points in the other direction. Thus, all the force quantities are additive, and one might as well just take the magnitude sum.)
|
| 65 | Click here to jump to the problem! | GR8677 #13
|
Electromagnetism }Maxwell's Equations }Maxwell's Equations
Magnetic monopoles remain a likeable (even lovable) theoretical construct because of their ability to perfectly symmetrize Maxwell's equations. Since the curl term has an electric current, the other curl term should have a magnetic current. (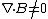 is taken to be obvious in presence of magnetic charge.) The answer is thus (D), and the revised equations are, is taken to be obvious in presence of magnetic charge.) The answer is thus (D), and the revised equations are,
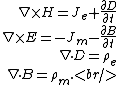
|
| 69 | Click here to jump to the problem! | GR8677 #36
|
Electromagnetism }Boundary Conditions }Boundary Conditions
The conductor perfectly reflects the incoming wave, and none is transmitted. The electric field is thus reversed. However, since E and B are perpendicular (related to each other by the Poyting Vector where the direction of propagation is given by the direction of 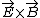 ), the magnitude of B is increased by 2, but its direction stays the same. ), the magnitude of B is increased by 2, but its direction stays the same.
Search on the GRE Physics Solutions homepage with keyword conductors for more on this.
|
| 70 | Click here to jump to the problem! | GR8677 #54
|
Electromagnetism }Faraday Law }Faraday Law
The induced current would act, according to Lenz Law, to oppose the change. In this case, since the field is decreasing (the wire is being pulled away from the field), the induced current would act to increase the field. On the side closest to the long wire, it would thus point in the same direction as the current from the long-wire. This eliminates all but choices (D) and (E).
Now, since the rectangular loop wire cannot induce a force on itself, the force is due to the field from the long wire. To the left of the loop, the long wire has a field pointing into the page, and thus the force there is left-wards. One can check again that choice (E) is right by right-hand-ruling the field on the right side of the loop. Since the field due to the long wire is again into the page, the force here is towards the right (since the current runs down the page on the right side of the loop).
|
| 72 | Click here to jump to the problem! | GR8677 #57
|
Electromagnetism }Faraday Law }Faraday Law
Faraday's Law has the induced voltage is given by the change in magnetic flux, as 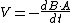 . (The minus sign shows that the induced voltage opposes the change.) . (The minus sign shows that the induced voltage opposes the change.)
Since the induced voltage has to be periodic (as the half-circle rotates around A), choices (D) and (E) are immediately eliminated.
The voltage changes from positive to negative in regions where the change in flux is slowing down, goes to 0, then speeds up again. Thus, choice (C) is out.
The change in flux is constantly increasing as the loop spins into the field, and it is constantly decreasing as it spins out of the field. This is choice (A).
|
| 74 | Click here to jump to the problem! | GR8677 #64
|
Electromagnetism }Gauss Law }Gauss Law
Gauss Law gives 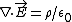 . Since the divergence of E in Cartesian coordinates is non-zero, there is a charge density in the region. QED . Since the divergence of E in Cartesian coordinates is non-zero, there is a charge density in the region. QED
|
| 76 | Click here to jump to the problem! | GR8677 #81
|
Electromagnetism }Resonant Frequency }Resonant Frequency
The maximum steady-state amplitude (after transients die out) occurs at the resonant frequency, which is given by setting the impedance of the capacitor and inductor equal 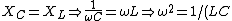) , as in choice (C). , as in choice (C).
|
| 78 | Click here to jump to the problem! | GR8677 #84
|
Electromagnetism }Accelerating Charges }Accelerating Charges
Elimination time:
(A) By the Larmor formula, one has 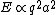 , where q is the charge and a is the acceleration. Since the charge is constant, this choice is true. , where q is the charge and a is the acceleration. Since the charge is constant, this choice is true.
(B) This is also true by Larmor's formula.
(C) True. The energy radiated through a perpendicular unit area is given by the Poynting vector.  \propto E^2\hat{r}-(\hat{r}\cdot\vec{E})\vec{E}) and and 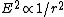 far away. Also, less rigorously, one can arrive at the same result from recalling the surface area of a sphere, far away. Also, less rigorously, one can arrive at the same result from recalling the surface area of a sphere, 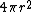 , and thus any term in , and thus any term in 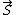 proportional to proportional to  will yield a finite, thus acceptable answer. (Thanks to the user astro_allison for this pointer. See p460ff of Griffiths, Introduction to Electrodynamics, 3rd Edition for more details.) will yield a finite, thus acceptable answer. (Thanks to the user astro_allison for this pointer. See p460ff of Griffiths, Introduction to Electrodynamics, 3rd Edition for more details.)
(D) False. It's a minimum in the plane.
(E) True, since far from the electron the field behaves as plane waves, with  and and 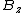 both 0. both 0.
|
| 80 | Click here to jump to the problem! | GR8677 #92
|
Electromagnetism }Frequency }Frequency
A three-pole magnet should produce three voltage peaks, and thus the frequency is 30 Hz. (Solution due to David Latchman.)
|
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
